Why always we see the same side of the Moon from the Earth?

The Moon is a small satellite of the Earth, constantly looking around the middle of it, really makes is to turn around the planet. It is very close to us and that is why there is mutual interaction between Earth-moon.

We always see the same face of the Moon because the Moon takes the same rotate once about herself that in giving a return around the Earth, a little more than 27 days. The result is that it always points towards us the same part of our satellite.


                                       


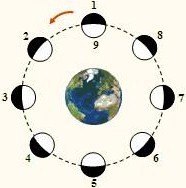
Here we can see the what happens to the moon  an why we always see the same part of the moon on it.




Sunni

ERATOSTENES

ERATOSTHENES

 Few days ago at class we were speaking about this caracter and I thought that will be interessant do a little search of he.

Eratosthenes was born in Cyrene (Libya) in 276 BC. He was astronomer, historian, geographer, philosopher, poet, mathematician and theater critic. He studied in Alexandria and Athens. He worked with math problems, such as duplication of the cube and prime numbers. He wrote many books which only have news for references of other authors.

One of his main contributions to science and astronomy was his work on the measurement of Earth. Eratosthenes in his studies of the papyri of the library of Alexandria, found a report of observations in Siena, about 800 km. Southeast of Alexandria, where he said that the Sun's rays to fall on a rod midday of the summer solstice, the current June 21, had no shadow.

Eratosthenes then made the same observations in Alexandria the same day at the same time, discovering that the Sun was vertically in a well of water the same day at the same time. He assumed correctly that if the Sun was at a great distance, its rays reach the earth should arrive at the same time, if this was flat as he believed in those times, and you should not find differences between the shadows cast by objects at the same time of the same day, regardless of where you will find.

However, to demonstrate that if they did, he deduced that the Earth was not flat, and using distance known between the two cities and the measured angle of shadows, calculated the circumference of the Earth at approximately 250,000 stadia, about 40,000 kilometers, fairly accurate for the time and resources.

 

This is a image from his theory

  

It's a photo of him

Sunni

Transcription of Aristotle and Mathematics
CONTEXT Aristotle was born in Stagira in 384 BC. And died in Calcis in 322 BC. At age sixty-two

His father was a well-known doctor who counted among his patients with the king of Macedonia Aristotle and the
Mathematics The Aristotelian logic or mathematical logic.
It is the discipline that deals with methods of reasoning. At an elementary level, logic provides rules and techniques for determining whether or not a given argument is valid. Logical reasoning is used in mathematics to demonstrate theorems. In computer science to check whether or not the programs are correct.

marcel rovi

 Los antiguos babilonios, genios matemáticos

Los antiguos babilonios, verdaderos genios en matemáticas, desarrollaron sus estudios matemáticos en base 60 en lugar de base 10. Por esta razón, un minuto tiene 60 segundos y un círculo tiene 360°.

fetaaa per eduuu !

curiosidades Perff Maths . ¡100! ¿100?

•  ¡100! ¿100?

• 123 - 45 - 67 + 89 = 100.
• 123 + 4 - 5 + 67 - 89 = 100.
• 123 - 4 - 5 - 6 - 7 + 8 - 9 = 100.
• 1 + 23 - 4 + 5 + 6 + 78 - 9 = 100.
• 

Publicacio feta per eduuu !!!!

Glossary

Hii! Today I'm going to do a little introducction of the new Unit that we're doing at class.

GLOSSARY

Square: It's geometric shape that has same four sides and all the inside angles of 90º degrees. If we know the longhitude of one side we can know the area and the perimeter.

Rectangle: It's a geometric shape that has two paralel sides different that the other two. It inside angles are of 90º degrees. And if we know the longhitude of two differents angles we can know the area and the perimeter.

Triangle:It's a geometric shape that has three side, if we addit all the insides angles, it wil be 180º degrees. It's the half of a square.

Rhombus: It's a geometric shape that has four sides and two diagonal of different longhitude. This two diagonals are perpendicular. This geometric shape has two  blunt and two acute angle. 


Rhomboid: It's a geometric shape that has four sides and two diagonal of different longhitude. This two diagonals aren't perpendicular. This geometric shape has two  blunt and two acute angle. 

Trapezium: It's a geometric shape that has four angles. Two sides are paralel and the other two aren't. It has two blunt and acut anles like the other two shapes saied before.


Trapezoid: It's a geometric shape that has four irregular sides.

Circle: It's a geometric shape that no has any side, it has a radius and diameter, it's the doubleof the radius. 

Sunni

mates incluso en la pizzaaaaa!!!!!!











Si tienes una pizza con un radio Z y una altura A, su volumen será: PI*Z*Z*A.



















publicacio feta per eduu!!! 

In chess there are situations that occur during the game that coincide with some theorems of mathematics, such as the famous rule of the square is no more than a practical application of the theorem of Pythagoras or the geometric definition of distance. In game theory, chess is considered a zero-sum game, and some go further by stating that for any position that can occur within the board there is a mathematical function capable of evaluating that position. Apart from the practical game, there is also a close relationship between these two areas. Who will not have read or heard the famous legend of the inventor and King, and the form of payments in grains of wheat proposed by the first, whose geometric progression within the chessboard reaches an impressive amount.

Not in vain has chess attracted the attention of famous mathematicians over time. The mathematician Carl. Gauss was interested in solving the problem of the 8 ladies. So also Leonard Euler, raised and solved the "problem of the movement of the horse" (to walk with the horse by all the squares of the board without going twice in any of them), besides proposing solutions inside the chessboard for the construction Of the magic squares of order n. It may seem incredible to the reader, but building the magic square gives the solution to the horse's journey!

Marcel Rovira

Es pot disfrutar d'una pel·lícula amb bastantes mates?

L'altre dia feien "El còdig Da Vinci" a la televisió, em vaig parar un moment i vaig pensar lo bé que m'ho vaig passar mirant aquesta peli, portant així bastantes mates. En un moment apareixen uns números que posteriorment els hi serveixen per averiguar un antic secret que a permés ocult miles d'anys.

Aquest números són: 1, 2, 3, 5, 8... Aquest números partenixen a Fibonacci i funciona així:

Tu comenses per l'1 i segueixes pel 2 un cop tens l'1 i el 2 els sumes que donen 3, després al 3 l'hi sumes el 2 que dona 5 i al 5 l'hi sumes el 3 que dona 8 i així succsesivament.

Això es sol trobar en forma d'un cargol:

Aixó enspot ajudar a entendre per exemplen en l'Auditori Nacional de Catalunya, que el sostra; de tal forma que aplican la succesio de Fibonacci ens perment que el so s'escolti bé desde qualsevol lloc de l'auditori.



També en altres coses es pot trobar, com en fenomens meteorològics:



O en política:





Albert Camps.

poligon

Triangle: polygon with three sides
Quad: polygon with four sides

Pentagon: polygon with five sides
Hexagon: polygon with six sides
Heptagon: polygon with seven sides
Octagon: polygon with eight sides
Enneagle: polygon with nine sides
Decagon: polygon with ten sides
Undecagon: polygon with eleven sides
Dodecagon: polygon with twelve sides
And so on…
Equilateral: if they have all their equal sides
Equiangle: if you have all sides equal
Regular polygon: if all sides are equal and equidangle (all angles equal)
Irregular polygon: it has both its sides and its unequal angles.
Convex: all interior angles are less than 180 °. By another method, it will be convex if for any pair of points in the polygon, the segment joining them is inside the polygon.
Concavo: some interior angle is more than 180º. Unlike the convex, in the concaves there is a pair of points of the polygon that the segment that unites them is outside the polygon.
Imple: no side of the polygon intersects with another
Complex: at least a couple of sides are cut




marcel rovira

Plane geometry. Etymologically, from the Greek "geo", earth; "Metrein", to measure, is the branch of mathematics that deals with the study of geometric figures in the plane. In general, in its elemental and classical form, the geometry focuses on metrical topics such as the calculation of the area and perimeter of flat figures and the area and volume of solid bodies. Other approaches to geometry are analytic geometry, descriptive geometry, topology, space geometry, with four or more dimensions, fractal geometry, ineuclide geometries.

Marcel rovira

Hello!
Today the grup of perffmaths will tell you our intentions to improve our jobs and publications, better quality, better quantity, better reflexions...
 Each of us will post something every two weeks.
We hope you that it like.

Albert C., Edu, Marcel i Sunni